The cost of conductor material is a vital part of the total cost of a transmission line. Therefore, the calculation of the conductor size of a transmission line is very important.
The economic size of conductor is determined by Kelvin’s law. It is used to find out the most economical area of x-section of a conductor for which the total annual cost of the transmission line is minimum.
Kelvin’s law can be stated as: The most economical area of x-section of a conductor is that for which the variable part of annual charges (i.e. annual charges on account of interest and depreciation) is equal to the cost of energy wasted per year.
Limitations of Kelvin’s Law in Power System
Although theoretically, Kelvin’s law holds good, in actual practice, an economical x-section of the conductor determined by Kelvin’s law may not suit because of the following factors:
1. Interest and depreciation on the capital cost outlay cannot be determined so accurately.
2. It is difficult to estimate the energy loss in the line without load curves, which are not available at the time of estimation.
3. It is also not easy to estimate the cost per unit of energy wasted in the line. The cost per unit of the energy wasted is not the same as that of the cost of generation per unit since their cost per unit depends upon load factors which are different for the generation and the line losses.
4. Kelvin’s law does not take into account various physical factors such as current density, mechanical strength, corona loss etc.
The conductor size determined by Kelvin’s law may not be practicable one because it may be so small that
- It may cause too much voltage drop in the line.
- It may cause high corona loss.
- It may be too weak from mechanical considerations.
Thus it is advisable to go to the larger conductor size irrespective to the economy.
To understand the kelvin’s law for the economic size of conductor properly, look at the following example.
Example: A 2-conductor cable 1 km long is required to supply a constant current of 200 A throughout the year. The cost of cable, including installation, is Rs. (20 a + 20) per metre where ‘a’ is the area of X-section of the conductor in cm2.
The cost of energy is 5 Paisa per kWh and interest and depreciation charges amount to 10%. Calculate the most economical conductor size. Assume resistivity of conductor material to be 1·73 micro ohm-cm.

Graphical illustration of Kelvin’s law
Kelvin’s law can also be illustrated graphically by plotting annual cost against the X-sectional area ‘a’ of the conductor, as shown in Figure. In the diagram, the straight line (1) shows the relation between the annual charge (i.e., P1 + P2a) and the area of X-section a of the conductor.
Similarly, the rectangular hyperbola (2) gives the relation between the annual cost of energy wasted and X-sectional area a. By adding the ordinates of curves (1) and (2), the curve (3) is obtained.
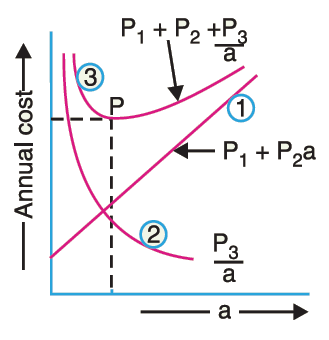
This latter curve shows the relation between total annual cost (P1 + P2a + P3/a) of transmission line and area of X-section a. The lowest point on the curve (i.e., point P) represents the most economical area of X-section.
Example: The cost of a 3-phase overhead transmission line is Rs (25000 a + 2500) per km where ‘a’ is the area of X-section of each conductor in cm2. The line is supplying a load of 5 MW at 33kV and 0·8 p.f. lagging assumed to be constant throughout the year.
Energy costs 4P per kWh and interest and depreciation total 10% per annum. Find the most economical size of the conductor. Given that specific resistance of conductor material is 10−6 Ω cm.
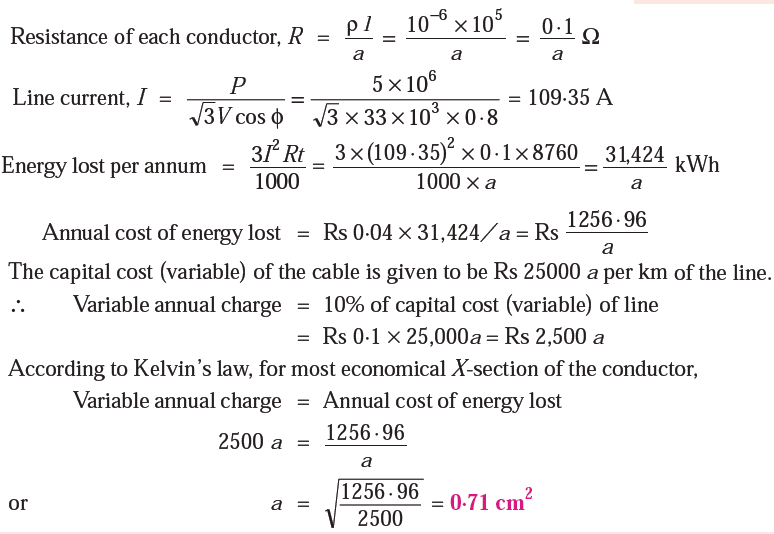
Related Posts
- Types of Poles in Transmission Line
- Overhead Line Insulators
- Voltage Distribution Over Suspension Insulator String
- Kelvin’s Law in Power System
- Skin Effect and Proximity Effect in Transmission Line
- Voltage Regulation & Efficiency of Transmission Line
- Corona Effect in Transmission Lines
Thanks for reading about the “kelvin law in transmission line”.