The Kirchhoff’s Laws are very useful in solving electrical networks which may not be easily solved by Ohm’s Law. In this article, I will describe the Kirchhoff’s current law and will show some kirchhoff’s current law examples to make this law easily understandable.

Kirchhoff’s current law states the following:

The summation of currents entering a node is equal to the summation of currents leaving the node.

An analogy that helps us understand the principle of Kirchhoff’s current law is the flow of water. When water flows in a closed pipe, the amount of water entering a particular point in the pipe is exactly equal to the amount of water leaving, since there is no loss.

In mathematical form, Kirchhoff’s current law is stated as follows:

Σ I_{entering node} = Σ I_{leaving node}

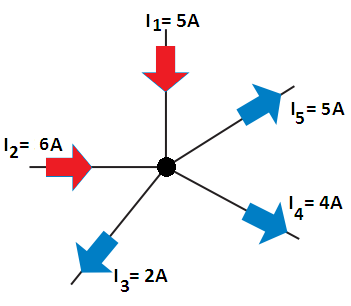
Figure 1 is an illustration of Kirchhoff’s current law. Here we see that the node has two currents entering, I₁ = 5 A and I₂ = 6 A, and three currents leaving, I₃ = 2 A, I₄ = 4 A, and I₅ = 5 A. Now we can see that above Equation applies in the illustration, namely,

Σ I_{entering node} = Σ I_{leaving node}

I₁ + I₂ = I₃ + I₄ + I₅

5 A + 6 A = 2 A + 4 A + 5 A

11 A = 11 A

When we analyze a given circuit, we are unsure of the direction of current through a particular element within the circuit. In such cases, we assume a reference direction and base further calculations on this assumption.

If our assumption is incorrect, calculations will show that the current has a negative sign. The negative sign simply indicates that the current is in fact opposite to the direction selected as the reference. The following example illustrates this very important concept.

Kirchhoff’s Current Law Examples

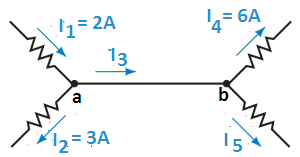
Example: Determine the magnitude and correct direction of the currents I₃ and I₅ for the network of Figure 2.

Solution:  Although points a and b are in fact the same node, we treat the points as two separate nodes with 0 resistance between them.

Since Kirchhoff’s current law must be valid at point a, we have the following expression for this node:

I₁ = I₂ + I₃

I₃ = I₁ – I₂ = 2 A – 3 A = –1 A

Notice that the reference direction of current I₃ was taken to be from a to b, while the negative sign indicates that the current is in fact from b to a.

Similarly, using Kirchhoff’s current law at point b gives

I₃  = I₄ + I₅

Which gives current I₅ as I₅  = I₃ –  I₄ = –1 A – 6 A = –7 A

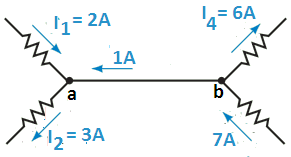
The negative sign indicates that the current I₅ is actually toward node b rather than away from the node. The actual directions and magnitudes of the currents are illustrated in Figure 3.

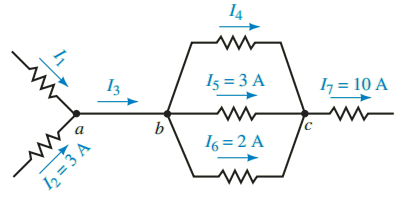
Example: Find the magnitudes of the unknown currents for the circuit of Figure 4.

Solution: If we consider point a, we see that there are two unknown currents, I₁ and I₃. Since there is no way to solve for these values, we examine the currents at point b, where we again have two unknown currents, I₃ and I₄. Finally, we observe that at point c there is only one unknown, I₄. Using Kirchhoff’s current law we solve for the unknown current as follows:

I₄  + 3 A + 2 A = 10 A

Therefore,

I₄ = 10 A – 3 A – 2 A  = 5 A

Now we can see that at point b the current entering is

I₃ = 5 A + 3 A + 2 A = 10 A

And finally, by applying Kirchhoff’s current law at point a, we determine that the current I₁ is

I₁ = 10 A – 3 A = 7 A

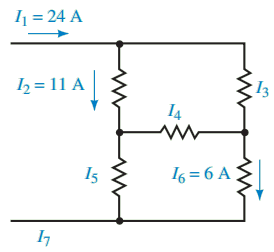
Example: Determine the unknown currents in the network of Figure 5.

Solution:  We first assume reference directions for the unknown currents in the network. Since we may use the analogy of water moving through conduits, we can easily assign directions for the currents I₃, I₅, and I₇.

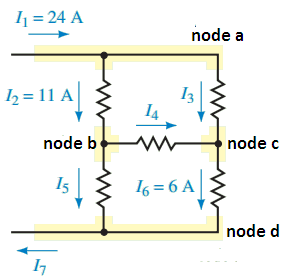
However, the direction for the current I₄ is not as easily determined, so we arbitrarily assume that its direction is to the right. Figure 6 shows the various nodes and the assumed current directions.

By examining the network, we see that there is only a single source of current I₁ = 24 A. Using the analogy of water pipes, we conclude that the current leaving the network is I₇ = I₁ = 24 A.

Now, applying Kirchhoff’s current law to node a, we calculate the current I₃ as follows:

I₁ = I₂ + I₃

Therefore,

I₃ = I₁ – I₂ = 24 A – 11 A = 13 A

Similarly, at node c, we have

I₃ + I₄ = I₆

Therefore, I₄ = I₆ – I₃ = 6 A – 13 A = – 7 A

Although the current I₄ is opposite to the assumed reference direction, we do not change its direction for further calculations. We use the original direction together with the negative sign; otherwise the calculations would be needlessly complicated.

Applying Kirchhoff’s current law at node b, we get I₂ = I₄ + I₅

which gives

I₅ = I₂ – I₄ = 11 A –  (-7 A) = 18 A

Finally, applying Kirchhoff’s current law at node d gives

I₅ + I₆ = I₇

Resulting in

I₇ = I₅ + I₆ = 18 A + 6 A = 24 A

Thanks for reading about “Kirchhoff’s current law examples”.