The primary and the secondary winding of an actual transformer have some resistance which is represented by R1 and R2 respectively (shown external to the windings in the figure). The resistances of the two windings can be transferred to any one side. It is done in order to make the calculations easy.
The resistance is transferred from one side to the other side in such a manner that percentage voltage drop remains the same on either side.
We can find the equivalent resistance and reactance of transformer by the short circuit test.
Equivalent Resistance of Transformer Formula
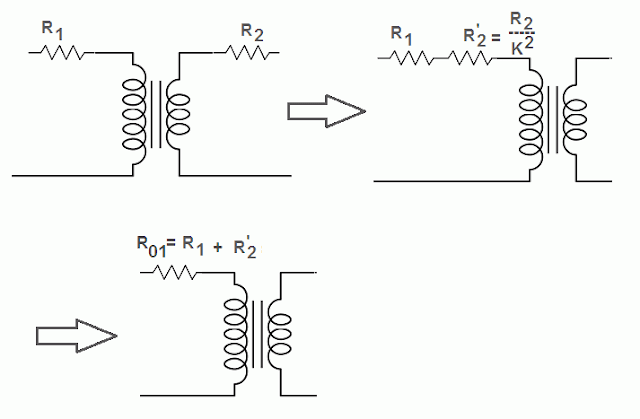
Let
R1 = primary winding resistance
R2 = secondary winding resistance
K = transformation ratio
Then,
Secondary resistance referred to primary R2’ can be calculated by the formula given below.
R2’ = R2/K2
The equivalent resistance of transformer referred to the primary is represented by R01.
Therefore, R01 = R1 + R2’ = R1 + R2/K2
Equivalent Resistance of Transformer Referred to Secondary
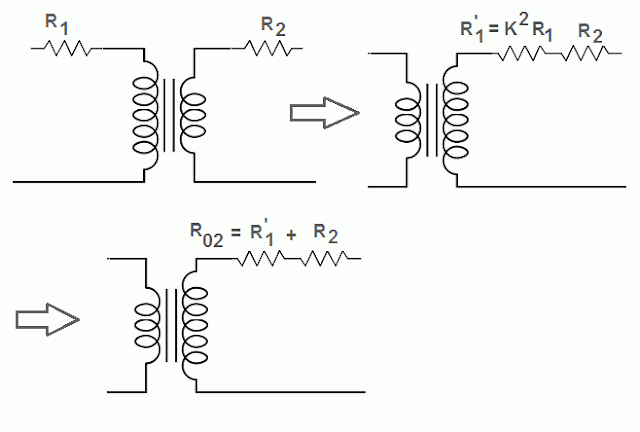
The primary resistance referred to the secondary is denoted by R1’ and can be calculated by the formula given below.
R1’ = K2R1
The equivalent resistance of transformer referred to the secondary is represented by R02.
Therefore, R02 = R2 + R1’ = R2+ K2R1
Equivalent Leakage Reactance of Transformer
The flux that links with both the windings of the transformer is called mutual flux and the flux which links only with one winding of the transformer is called leakage flux.
Due to leakage flux of the primary winding and the secondary winding, an EMF is induced in the respective winding. The primary and secondary voltage will have to overcome these induced EMFs. Thus these induced EMFs are considered as the voltage drops across the factitious reactances placed in the series with the primary and secondary windings. These reactances are called as the leakage reactances and they are shown in the figure.
As done in the case of resistances, the reactances can also be transferred to either side. The reactance from one side to other is transferred in such a manner that percentage voltage drop remains the same on the either side.
Equivalent Reactance of Transformer Referred to Primary
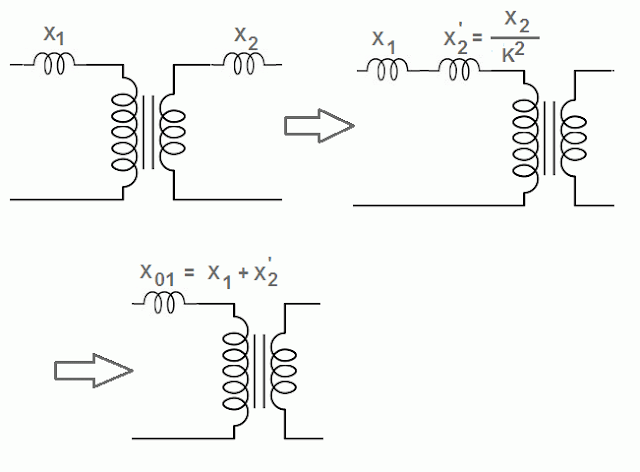
Let
X1 = primary winding reactance
X2 = secondary winding reactance
K = transformation ratio
Then,
Secondary reactance referred to primary X2’ can be calculated by the formula given below.
X2’ = X2/K2
The equivalent reactance of transformer referred to the primary is represented by X01.
Therefore, X01 = X1 + X2’ = X1 + X2/K2
Equivalent Reactance of Transformer Referred to Secondary
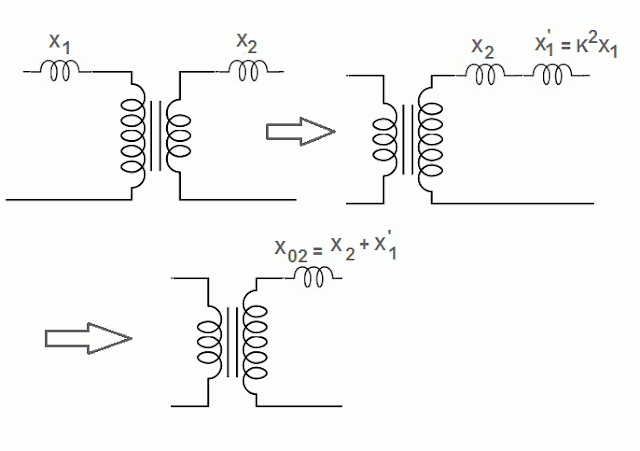
The primary reactance referred to the secondary is denoted by X1’ and can be calculated by the formula given below.
X1’ = K2X1
The equivalent reactance of transformer referred to the secondary is represented by X02.
Therefore, X02 = X2 + X1’ = X2+ K2X1
Impedance of Transformer
The primary impedance Z1 = R1 + jX1
And secondary impedance Z2 = R2 + jX2
The transfer of impedances takes place on the same lines as that of the resistances. The transfer of impedances can take place from primary to secondary and vice versa.
Z01 = (R012 + X012)1/2 impedance referred to primary side.
Z02 = (R022 + X022)1/2 impedance referred to secondary side.
Transformer | All Posts
- Ideal Transformer
- Construction of Three Phase Transformer
- Types of Transformers
- Equivalent Resistance and Reactance of Transformer
- Equivalent Circuit of Single Phase Transformer
- Power Loss in a Transformer
- Open Circuit Test of Single Phase Transformer
- Short Circuit Test on Single Phase Transformer
- Transformer Efficiency
- Regulation of Transformer
- Autotransformer
- Instrument Transformers
- Polarity of Transformer Windings
- Significance of Vector Group of Transformer
- Buchholz Relay Construction | Working
- Why current transformer secondary should not be opened
- Dielectric Strength Test of Transformer Oil
- Transformer Moisture Removal Process
© https://www.yourelectricalguide.com/ equivalent resistance of transformer.